
(一)定势与功能固着
定势又称心向,本来泛指个体对一定活动的预先准备状态,后来特指在问题解决中由于以往惯用某种方式解决问题而在遇到同类问题时也会重复同样做法的思维习惯性倾向。而功能固着属于定势的特例,是指个体习惯了只从物体某一常用功能角度出发思考物体作用的定势。证明定势和功能固着对问题解决的障碍作用的经典实验分别是卢钦斯(Luchins,1932)的量水实验(水罐问题)和Duncker(1945)的蜡烛问题。
表征问题的方式至少有以下几种
1.符号
用数学符号来表征语言描述不失为一种有效的表征方式,但一定要保证符号间数量关系的准确性。如Simon(1986)出题“学校食堂卖馒头和包子,每人只能买一个;若四人买馒头,就的有五人买馒头,这样才能全部卖完。请用S代表包子、C代表馒头,写出馒头与包子的数量关系。”结果63%的美国被试和38%的中国被试写成了错误的5S=4C(应该为4S=5C)。
2.列表
将复杂的众多关系以表格形式列出可能有助于从中一眼看出要找的一对关系,但这种列表还可以分为对偶式列表、网络式列表、矩阵式列表等几种。如:
甲、乙、丙、丁从左至右依次坐在桌前,并且,
(1)甲穿蓝衬衫
(2)穿红衬衫的人拥有自行车
(3)丁拥有摩托车
(4)丙靠着穿绿衬衫的人
(5)乙靠着拥有小轿车的人
(6)穿白衬衫的人靠着拥有摩托车的人
(7)拥有三轮车的人距拥有摩托车的人最远
问:谁拥有小轿车?
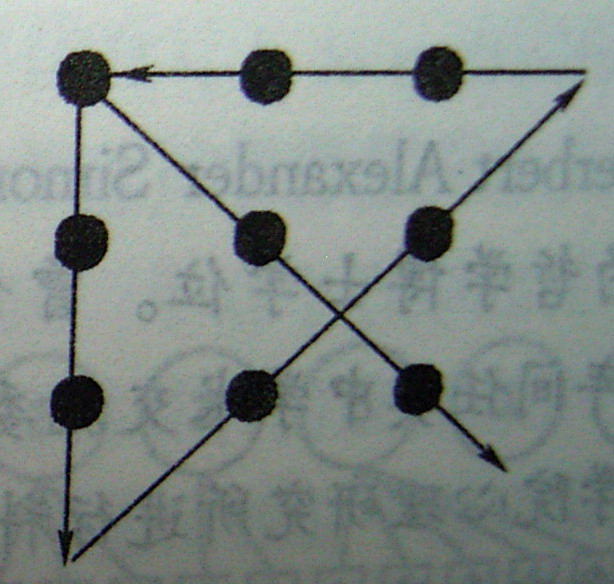
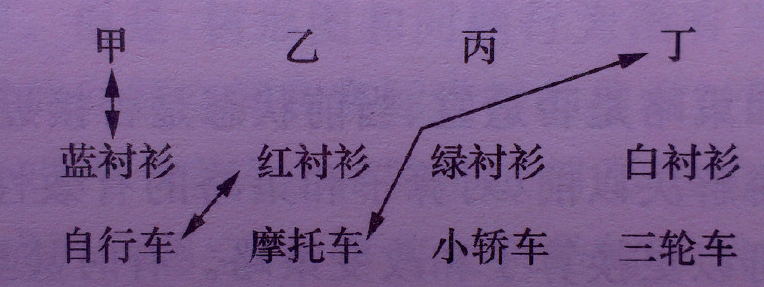
这个问题的三种列表方式如图1所示,其中图2是对偶式列表、图3是网络式列表、图4是矩阵式列表。有研究表明,矩阵式列表对解决这类关系问题最有效。
 |
 |
 |
 |
图1 |
图2对偶式列表 |
图3网络式列表 |
图4矩阵式列表 |
Simon(1986)发现,许多学生利用画图的方法来解决如下问题(见下图);若只用语言而不用图形来表征问题,解决问题就会遇到较大困难。
在一个两边直径相等的U形管子里装上水银,此时水银处于同一水平。若往管子右边灌入14厘米的水,问左边的水银比原来升高了多少(已知水银密度是水的14倍)?
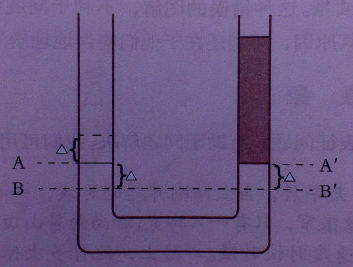
U形管水银实验
Keren(1984)实验中的问题是:
有三个硬币,用抽牌的办法分给小红和小明:若抽出红牌,钱归小红;若抽出黑牌,钱归小明;直至硬币分完。问下述哪种情况最可能发生?
(1)一人得三个硬币,另一人一个没有;
(2)一人得二个硬币,另一人得一个;
(3)(1)与(2)的可能性相等。
若采用列表式方法表征问题,被试就可能列出四种结果:①小红3、小明0;②小红0、小明3;③小红2、小明1;④小红1、小明2,从而得出(1)、(2)可能性相等的错误答案。
而若采用下图所示的图解方式,正确回答问题的概率就会升高。Keren在实验中也的确发现了用列表的被试者中只有40%能正确解决问题、而用图解的被试中80%的人都正确解决了问题。
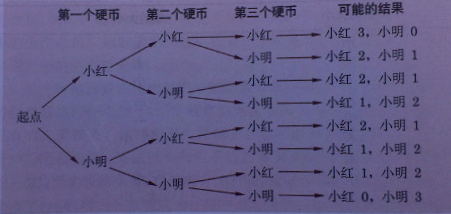
图解表征问题

早上太阳升起时,一个和尚开始爬山朝圣。山路很窄,只有一脚宽,和尚只能沿路走、不能往旁边迈步。他一路时快时慢、多有休息和进食,近日落时到了山顶庙中礼佛。第二天,就象来时一样日出启程,和尚开始下山。照样时快时慢、多次休息,于日落黄昏时到达山脚。请问:和尚在往返路上是否可能在两天中的同一时刻在同一地点通过?
1.知识与经验
有证据表明,丰富的知识与经验可以使问题解决者超出给定的信息进行推测,从而提高解决问题的可能性。总的来说,专家与新手相比,其知识的作用表现在三方面:
(1)问题表征的精细化
如第五章第三单元“短时记忆的容量”部分所述一样,精细化的知识可使得专家在短时间内以组块形式存储和提取更多的内容。
(2)解决问题策略的合理化
研究表明,专家与新手在解决问题时间上的差异除表征问题外,还存在于解决问题的方向与焦点上。专家惯用向前推理,即爬山法;而新手反过来倾向于选择向后推理或手段-目的分析。
(3)自动的专业加工
专家能使他们在问题解决中轻松提取和执行的各种操作变成自动加工,因而会更好地监控自己的加工过程及问题解决中的正确率变化,从而使问题解决变得高效而准确;而新手则必须利用他们的工作记忆来努力保持问题的多项特征以及各种有效策略,这就导致牺牲了很多原本用于监控的资源,最终影响到问题解决的效率。
2.注意与酝酿效应
分链子问题
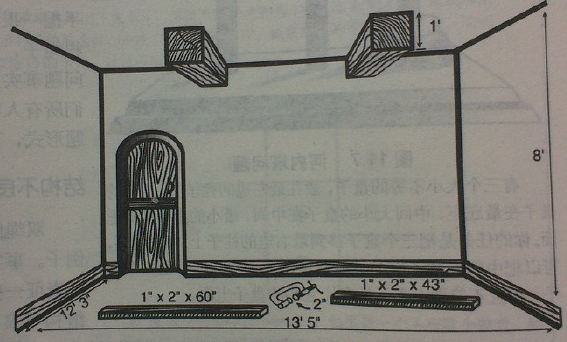
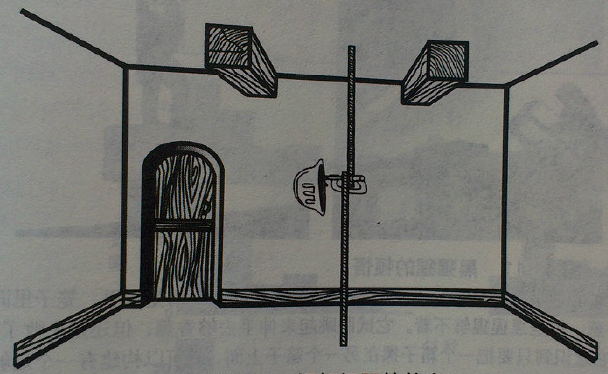
问题的难度可以包括问题空间的大小、问题的结构特点、问题的复杂性及无关信息的干扰等许多方面,通常问题难度越大,有效解决问题的可能性就越小。比如(成分与转换的多少[黄])