
三、问题解决的策略
问题解决策略是影响问题解决效率的重要因素之一,也是认知心理学关于问题解决研究的重中之重。例如“9+3+2+7+8+1=?”这道算题,既可以用平常的按顺序连加方法算出,也可以将数字两两成10、再算出共有几个10。第一种方法被称为“算法”策略,第二种方法是“启发法”策略,往往能更快速有效地解决问题,认知心理学通常就将问题解决的策略分为这么两大类。
(一)算法
指在问题空间中,随机搜索所有可能的算子或途径,或按照以往成形的逻辑步骤按部就班找出答案的过程。双色三盘密码锁问题一般就采用算法来解决,即有三个小转盘组合成的密码锁、每个转盘都有红绿两色选择,密码排列“红绿绿”是保密的,而目前锁的位置是“红红红”;为了打开密码锁、找到正确的颜色组合,可以在头脑里将所有可能的三盘排列顺序按规律一一变化、呈现出来,再逐一搜索、尝试,就会解决问题。(如下图所示)
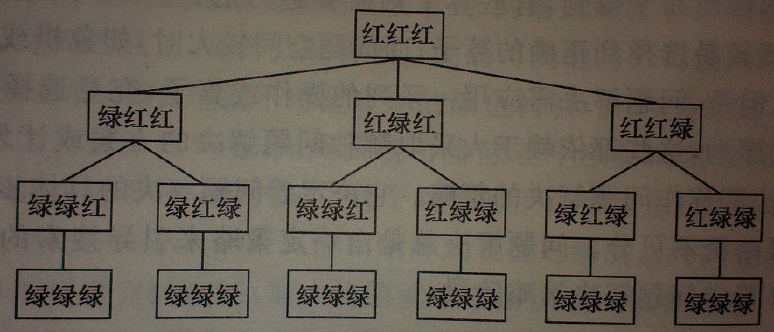
双色三盘密码锁的算法示意图
(二)启发法
在本章第二单元第四部分的“推理的策略与逻辑”中,已经介绍过启发式这种思维策略。它是指人们凭借经验等形成的快速推理或解题思路,并不能保证一定得出正确结论或正确解决问题,但却往往能让人快捷、有效的进行推理或解决问题。而在问题解决中常用的启发式策略主要包括以下几种。
1.手段-目的分析
指发现问题空间中问题初始状态与目标状态间的差距、再设立几个缩小这种差距的子目标,通过算子不断实现一系列的子目标、并最终达到总目标的方式。这种策略实行的关键就是设立合理的子目标,也就是将一个大问题分成了几个更好解决的小问题,再将它们联系在一起。如上面提到的“河内塔”问题,如果需要移动的圆盘是五个的话,我们不妨先用两个圆盘试试,再增加到三个盘、四个盘,以发现圆盘数与移动方向和次数的关系,这就是几个子目标。事实上河内塔任务的最佳完成步骤是有规律的,如果不想走冤枉路的话,圆盘总数为奇数时要先将最小的圆盘挪到目标柱上、而圆盘总数为偶数时要先将最小的圆盘挪到除起始柱与目标柱外的另一柱上;整个河内塔任务的最少移动次数是2n-1。所以,也可以将寻找相对较小的圆盘往哪个柱子上移动的规律和怎么把较大的圆盘移出起始柱作为子目标。
2.向前推理
也叫“爬山法”,可算是手段-目的分析法的一种变式,当我们一时设立不出合理的子目标或从起始状态到目标状态的算子系列太多太复杂时,我们不妨从现有状态可以进行的演变步骤出发试着往前走,几步之后再停下来瞧瞧,比较一下这时与目标状态的差距是否缩小了,这样以渐进的步子向目标状态靠近。这就象爬山一样,一开始可能登山者并不知道所选的路径是否正确,只能走着瞧,走一会儿后再看离山顶是否更近了;如果发现越走越远,还可以退回到最近的岔路口、选择另外的途径。比如前面讲到的“野人和传教士过河”问题,根据规则和现有条件,第一步只能是让两个人而不是一个人过河,因为一个人过去后还得再划船回来,等于白做工!而两个人是选两个传教士还是两个野人或是一样一个,则可以试着其中一种选择走下去再看了。
3.向后推理
也称“逆推”或“逆向工作”、“反向搜索”等,即从问题的目标状态倒着往回走,直至达到起始状态。解几何题一般较适合这种策略,如已知矩形ABCD(见下图)、求证对角线AD=BC,可以认为“要想证明AD=BC,就先要证明△ACD≌△BDC”;接下来顺理成章“要证明两个三角形全等,必须先证明∠ACD=∠BDC、AC=BD、AB=CD”;由于ABCD为矩形,最后一个条件得以满足,所以再把上述逆推的步骤顺着完成,就能解决问题了。
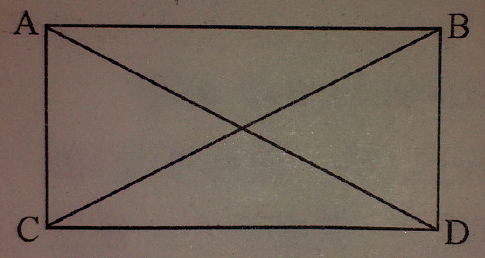
一道几何题

有10个棋子,两人轮流拿;一人每次可拿1-3个棋子,谁最后拿谁输。请问你有无方法保证赢此游戏?(教师视角)
4.类比迁移
也称类推,就是将要解决的新问题(称为“目标相似物”)与以前解决过的问题(称“基础相似物”)相比较、找出相似性,并以以前解决这类问题的相似方法来解决当前问题。比如Duncker(1945)的实验中使用了一个问题:
某胃癌患者,经医生确诊不能开刀切除,唯一治疗途径是用放射线破坏癌体组织。但采用发射疗法遇到的困难是,如果放射线强度不够,就不足以破坏癌体组织;而若其强度足够,则放射线在破坏癌体组织之前就会损伤其他部位的健康组织。那么在两难情况下,怎样才能既不伤害健康组织、又达到治疗的目的?
当时只有5%的大学生被试选择了“使放射线经过健康组织时强度减弱”这样的正确解题方式。但Gick等人(1980)在自己的实验里发现,如果让被试在解决上述治疗胃癌问题之前先学习下面一道类似的问题,则100%的被试正确解决了治疗胃癌问题。
一位军官接到命令要去进攻一个敌人的堡垒,而堡垒四周呈放射状遍布许多直达堡垒的小路,路边住着普通百姓。军官面临的问题是:如果集中火力从一个方向发动攻击,则路边的老百姓将遭受严重损伤。于是他决定分兵从小路进攻,待各路队伍接近堡垒时再集中火力、猛烈进攻。结果堡垒被攻克了,百姓也没有受到伤害。
很明显Gick实验中的被试从军官攻打堡垒的经验中得到了启发,通过类比找到了治疗胃癌的安全方法。上面讲“逆推”策略时给大家做练习用的10棋子问题,在逆推中也存在着类推。
5.简化
也可称“计划”或“简化计划”。解决问题时,人们常可抛开问题的某些方面或部分而抓住主要结构,把问题抽象成较简单的形式;先解决这个简单问题,再借助已得出的答案帮助或指导更复杂的整个问题的解决。比如已知下面5个方程,要求出X和Y的函数关系:
R = Z+2
X = R+3
2M = 3L+6
Y = M+1
R = 3L
我们可以先将5个方程简化为:
R - Z
X - R
M - L
Y - M
R - L
这有助于看出变量间的关系,并从中抽取出联结X和Y的途径:X-R-L-M-Y。只要把原始方程代入这个联结途径,问题就可以解决了:
X = R+3
= 3L+3
= 2M-6+3
= 2(Y-1)-6+3
= 2Y-5