三、短时记忆的容量
    （一）短时记忆容量有限
    1.大小：通常认为是5-9个左右
    神奇数字7±2的发现和其他研究
    早在19世纪中叶，爱尔兰哲学家William Hamilton据说曾观察到，如果将一把弹子撒在地板上，人很难一下子看到超过6-7个弹子。1887年，Jacobs做过一个实验，他给被试大声念出一系列无特定顺序的数字，然后要他们立即写下他们能回忆出的全部数字。结果发现，被试能够回忆出的数字的最大数量约为7个。Ebbinghaus也发现，阅读一次可记住7个无意义音节。从20世纪50年代开始，许多心理学家应用字母、音节、字词等各种不同材料进行过类似的实验，所得结果是一致的，即短时记忆的容量约为7。1956年，美国心理学家George A. Miller发表了一篇著名论文《神奇数7加减2：我们加工信息的能力的某些限制》，明确提出短时记忆容量为7±2，即一般为7并可在5-9之间波动。这个看法为大量实验所证实并得到公认。
    2.单位：组块
    短时记忆能记7个左右的既不是笔画或字也不是单词或数字，而是组块，即将若干较小单位（如字母）联合而成熟悉的、较大的单位（如字词）的信息加工过程及这样所组成的单位（Miller，1956）。
    正因为短时记忆的单位是组块而不是字母或单字，所以我们的短时记忆能记住的内容远远不象我们想像的那样少。比如“吉林省长春市东北师范大学网络课程”这个短语一共16个字，如果每个字就是一个组块的话，你一下子是记不下来这个短语的；但我们可以根据语义经验把它分成“吉林省”、“长春市”、“东北师范大学”、“网络课程”四个组块，那就能做到一步到位记住它了。
    组块还可以细分为以下两种形式：
    （1）意义组块：运用长时记忆中已贮存的知识形成的较大的有意义的单元。如刚才的短语记忆方法。
    （2）时空组块：把时间空间上接近的一些项目分为主观的几组，叫分组，分组后形成的组块就是时空组块。
    前面提到的“短时记忆容量为7±2”的情况一般是指实验中的每个字母或数字就是一个组块，而我们日常生活中通常不是这样的，我们基本都利用了意义组块或时空组块。
    本章开篇的“别有用心”里提到了电话号码18645186316的记忆，如果你按照通常记手机号的方法——前3个数字+中间4个数字+后4个数字——来记的话，你就属于使用了时空组块的记忆术记了3个组块，比单纯死记硬背11个数字（相当于11个组块）肯定要快和牢；如果你按照这串数字的特有规律记成“186-45186-316”的话（即3-5-3记法），你就在时空组块的基础上搀杂了一定的意义，虽然还是记3个组块，却比单纯的时空组块记忆效果又要好上一些；而如果你记成“摇摆喽-是我摇摆喽-闪腰喽”……我想你就更不会忘了这个电话了！这既是组成3个意义组块的记忆方法，也是符合本章第一单元“加工层次”理论里提到的“精细的整合性复述”的要求，从而能保证不仅短时记忆记得快、而且短时记忆的信息更可能进入长时记忆并记得长久。
    3.影响短时有限容量的因素
    我们可能发现了，即使大家能记住的组块数量都一致，但每个人仍然在短时记忆力上有着巨大差异。这就跟以下一些因素有关了：
    （1）组块大小：如果增加每个组块本身包含的信息，那么能记住的短时记忆的组块数量就随之减少；但总体能记住的知识量可能反而还增多。比如：一个小学生半分钟内能记7个双字词（如“太阳”、“花草”），那他同样时间里大概只能记5个四字成语（因为根据小学生的语文水平，每个双字词或是四字成语只能是一个组块）。虽然记住的组块数减少了两个，可记住的字的总数却多了（14∶20）。
    （2）组块类型：意义组块记忆容量好于时空组块。
    （3）人的认识经验：个体知识经验越丰富，越能使每一组块包含更大的信息数量，而仍保持总的组块数不变。象上面那个小学生记词的例子，如果换成文化水平高一些的成年人，则可能无论记双字词还是四字成语，都能记7个。

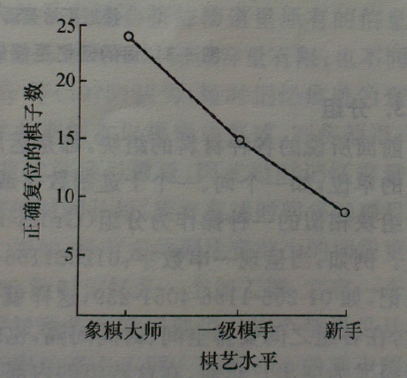
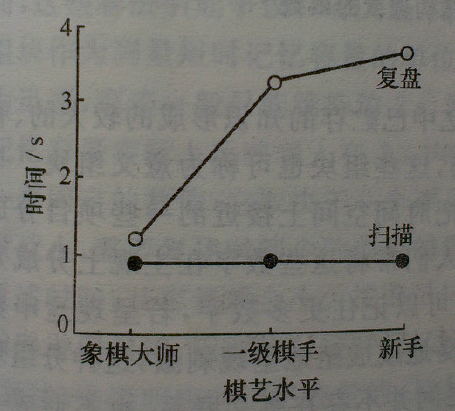
    象棋的复盘，这就是专家与新手的区别
    Chase和Simon（1973）以象棋大师、一级棋手和象棋新手为被试，做了一系列有关象棋复盘的实验。比如给他们呈现一个包含25个棋子的真实棋局5秒，撤去这个棋盘后要求他们根据记忆在另一棋盘上重新恢复刚看过的棋局；结果表明（见左图），象棋大师可正确复位的棋子数最多，一级棋手次之、新手最少。这是为什么呢？是因为象棋大师眼快、手快还是他们一下子能记住更多棋子的位置？Chase等人在另一项象棋复盘的研究中分别记录了上述被试扫视和复盘所用的时间，发现象棋大师、一级棋手和新手在扫视时间上没有什么差别，但象棋大师用于复盘的时间却明显地少于一级棋手和新手（见右图）。这说明象棋大师在相同的时间内看到和记住的棋子数比一级棋手和新手都要多。更有意思的是，Chase和Simon还对实验结果进行了组块计算，即他们认为被试复盘时一个个摆棋子所表现出的两类时间间隔可以计算出组块来：一类时间间隔是2秒，可看作组块间的间隔；另一类是少于1秒，应该是组块内各成分的时间间隔。据此计算，象棋大师、一级棋手和新手在各次实验中的平均组块数分别是7.7、5.7和5.3；每个组块中棋子的平均数为2.5、2.1及1.9。这说明棋艺水平越高的棋手应用的组块越多、且每个组块所包含的成分也越多；尤其是象棋大师，在给定的时间内利用组块可获得和记住更多的信息。但在另一项研究中发现，如果给他们呈现的是随机放置的棋子，则象棋大师也和一级棋手或新手一样，只能正确复位6个左右的棋子了。这时象棋大师无法运用其已有的知识经验进行组块，其优势也就不复存在了。由此可见，经验在组块形成和提高记忆效果上有着怎样重要的作用。

    （4）不同性质的材料：材料性质不同，短时记忆容量不同，这可能与不同材料的复杂度、加工速度、可以组成组块的类型及数量不同等因素有关。下图是Cavanaugh（1972）研究出的部分不同类别材料的短时记忆容量与加工速率。

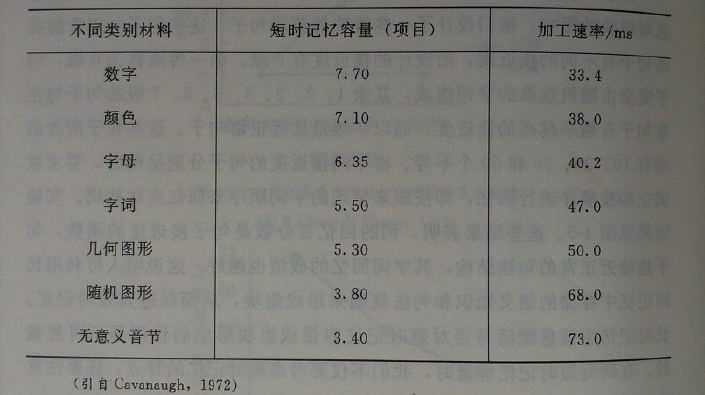
    4.短时记忆容量有限的原因
    为什么短时记忆容量要有限制呢？目前主要有从“系统论”与“加工论”两个角度出发进行的解释以及将二者合并的第三学说三种理论。
    （1）存贮有限说 （相当于记忆的“系统说”）
Waugh、Norman（1965）和Atkinson、Shiffrin（1968）认为，短时记忆是槽道贮存，由于槽道数量有限而每个槽道只能贮存一个组块，所以记忆容量有限。
    （2）复述回路说（相当于记忆的“加工说”）
    Baddeley（1975）认为短时记忆是一个加工器，它有一个复述回路专司复述。而短时记忆痕迹的衰退极为迅速（2s），如果不及时加以再现或复述，则马上消退。因此，短时记忆容量实际上反映着人在2s内能够加以复述的项目数量。也因此短时记忆容量没有固定数值，它取决于一个项目复述所需时间的长短，需时少的项目容量就大，反之则小。
    （3）贮存与加工权衡说 （相当于“系统说”和“加工说”的整合）
    Klatzky（1975）认为短时记忆是一个工作台，空间有限，如果贮存项目多，则占据的空间就多，留给操作的空间就少。反之，操作的空间多，可以贮存的项目就会少。所以，短时记忆体现了贮存与加工之间的权衡。