实验原理

液体表面层分子和内部（本体）分子受力情况不同。图10-1是与蒸气呈平衡的纯液体（图中圆圈代表分子的引力范围），内部分子(图中A)受到周围液体分子的作用力相互抵消，合力为零。而表面层分子（图中B、C）受到液相和气相分子引力，合力指向液体内部，要使液体内部分子移到表面层（使液体的表面积增大），就必须克服此吸引力作功。

 
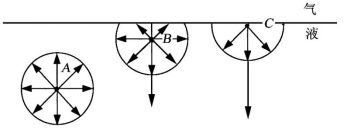
图10-1 液体分子的受力情况

 

在恒温恒压下，可逆地增加液体表面积As，系统自由能G的改变为：

                            （1）

则                                （2）

式中是增加单位表面积时所需的可逆功，也就是单位面积的表面层分子比相同数量的内部分子多出的自由能，称为比表面自由能，单位为J·m-2。

由于表面层分子受到内部分子的引力，因而表面层分子有自动进入液体内部的倾向。在宏观上表现为有一个与表面平行，力图使表面收缩的力。从这个角度来理解的物理意义时，又称为表面张力，单位N·m-1。表面张力的大小与液体的本性、共存气相、温度和压力有关。当温度升高时，表面张力下降，当达到临界状态时，表面张力趋于零。
在纯液体中加入某种溶质形成溶液后，溶剂的表面张力会升高或降低。若加入溶质使溶液的表面张力降低，则表面层中溶质的浓度大于溶液本体的浓度；反之，若使溶液的表面张力增加，则表面层中溶质的浓度小于溶液本体的浓度。当然，表面层与溶液本体的浓度差又会引起溶质分子的扩散，当这两种相反的趋势达到平衡时，溶液表面层与溶液本体的组成不同，这种现象称为溶液的表面吸附。在一定的温度和压力下，溶液的表面吸附量与溶液的表面张力和浓度有关。对于二组分稀溶液，它们之间的关系满足吉布斯等温方程：

                              （3）

式中为表面吸附量，为表面张力，c为溶液浓度，T为热力学温度，R为气体常数。若 <0时，则>0，称为正吸附；反之， >0，则<0，称为负吸附。从上式可以看出，只要测定溶液表面张力与浓度的等温曲线，通过曲线的斜率可求得各浓度下溶液的表面吸附量。

对于单分子吸附，其吸附量与浓度c之间的关系可用朗格缪尔（Langmuir）等温吸附方程表示，即

                              （4）

式中为饱和吸附量，a为吸附平衡常数。将此式两边取倒数可整理成线性方程：

                            （5）

以对c作图应为一直线，其斜率m为，若以N代表饱和吸附时单位表面层中的分子数，则。L为阿伏加德罗常数。在饱和吸附时，每个被吸附分子在表面上所占的面积，即分子的截面积S为：

                                  （6）

若已知溶质的密度ρ，摩尔质量M，就可计算出吸附层厚度，即分子的长度δ为

                                 （7）
             

 

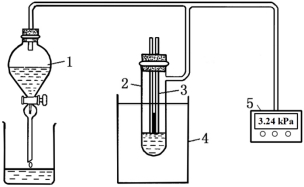
图10-2 表面张力的测定装置                          

1-抽气用的滴液漏斗；2-样品管；3-毛细管；4-恒温槽；5-数字压力计

本实验采用最大气泡压力法测定液体的表面张力，其测量装置如图10-2所示。将待测表面张力的液体装入样品管2中，使其中的液面与毛细管3端面相切，则管内液面沿毛细管上升。通过调节滴液漏斗1的活塞使系统缓慢减压，此时由于毛细管3内液面上方的压力（即外压）大于样品管中液面的压力，故毛细管内的液面逐渐下降，当液面至管口时便形成气泡逸出。此时压力计5的压力差Δp即为待测液体在毛细管中所受的附加压力，即

Δp =                                  （8）

式中R'为气泡的曲率半径，因毛细管半径很小，所以形成的气泡基本上是球形。气泡刚形成时表面几乎是平的，此时曲率半径中R'最大（如图10-3所示）；当气泡形成半球形时，R'与毛细管半径r相等，曲率半径达最小值，此时Δp为最大值。随着气泡的进一步增大，R'又趋增大，直至逸出液面。

                            

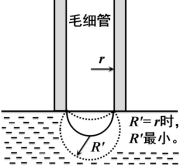
图10-3 气泡形成过程示意图

在此过程中，最大附加压力可以用DP-AW精密数字压力计5测量表示。则

                            （9）

由（9）式，得

                        （10）

式中称为仪器系数，对于给定的毛细管，K为常数。可以用已知表面张力的溶液作为标准，由实验测定，由（10）式求出K。本实验以水作为标准，则，因此待测液体的表面张力的计算式为

                          （11）