1. 如果遇到暂时解不开的题,你会怎么做?
教师视角:当然是停下来,把题放一放,最少可以放松或从事其他活动半个小时。根据酝酿效应的启示,磨刀不误砍柴功,适当的停顿可以转换思路和注意、有益于发现潜在的问题条件或要素,也利于无意识思维发挥作用。此外,Mayer(1992)等人更提倡“具体化”和“爆炸”的作用。前者指把抽象问题转换成具体表征,如解决卢钦斯的量水问题时亲自用茶杯来试一试,这就类似于把“和尚爬山”问题转化成表象形式来解决,可以提高理解问题的可能性;后者指大量爆发思路,打破刻板的定势和功能固着,哪怕有些思路看起来是那么的荒谬可笑、不可思议。无论是“知觉爆炸”(对问题从不同角度给出尽量多的不同的定义和看法)还是“情绪爆炸”(勇于冒险、不怕失败地提出见解甚至大声说出各种想法),都能克服思考中的障碍、促进问题的解决。
2. 请将下面火柴拼成的图(见下图)只挪动其中三根火柴就将其组成四个正方形。你觉得怎样才能提高解决这道题的效率?而要用6根火柴组成4个三角形,你会怎么做?
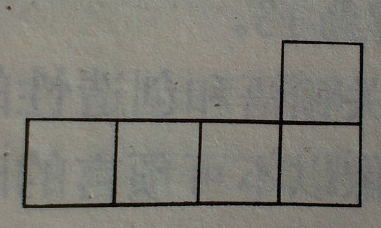
一个火柴问题
教师视角:挪动火柴的步骤如图所示。当然你可能是以别的方式解决的这道问题,但解决这道问题的关键在于对问题的表征方式。这类问题都被通称为“火柴问题”,它们通常是被要求用几根火柴拼出一些简单的几何图形,或是改变一下现有的火柴图形变成另一种简单图形。我们不妨从简单几何图形的构成来思考,三角形是三条边、正方形是四条边……如果每根火柴都用作了一条边的话,那么三角形需要3根火柴、正方形需要4根火柴……可经常火柴的数量少于简单图形的边数,那就说明有时需要用一根或几根火柴做公共边(如上图中的图形就是16根火柴组成了5个小正方形,共有4条公共边)。那么我们计算一下四个正方形需要多少条边?16条;而火柴有多少根?16根。那么我们就要挪动火柴、使得没有一根火柴被共用成为公共边就行了。用6根火柴组成4个三角形的题目同理可解(12条边需要每根火柴都是公共边)。当然,该问题还存在一个打破思维定势、从三维空间想问题的策略(见图)。

Katona(1940)火柴问题的解法

火柴组成的立体图形