色谱分析的目的是将样品中各组分彼此分离，组分要达到完全分离，两峰间的距离必须足够远。两峰间的距离是由组分在两相间的分配系数决定的，即与色谱过程的热力学性质有关。但是两峰间虽有一定距离，如果每个峰都很宽，以致彼此重叠，还是不能分开。这些峰的宽或窄是由组分在色谱柱中传质和扩散行为决定的，即与色谱过程的动力学性质有关。因此，要从热力学和动力学两方面来研究色谱行为。

一．塔板理论

（一）分配平衡

1．分配系数

描述这种分配的参数称为分配系数见它是指在一定温度和压力下，组分在固定相和流动相之间分配达平衡时的浓度之比值(K)。

（12－9）

分配系数是由组分和固定相的热力学性质决定的，是每一个溶质的特征值，它仅与两个变量有关：固定相和温度。与两相体积、柱管的特性以及所使用的仪器无关。

2．分配比

分配比又称容量因子，它是指在一定温度和压力下，组分在两相间分配达平衡时，分配在固定相和流动相中的质量比。即

（12－10）

k值越大，说明组分在固定相中的量越多，相当于柱的容量大，因此又称分配容量或容量因子。它是衡量色谱柱对被分离组分保留能力的重要参数。k值也决定于组分及固定相热力学性质。它不仅随柱温、柱压变化而变化，而且还与流动相及固定相的体积有关。

分配比k值可直接从色谱图测得。设流动相在柱内的线速度为u，组分在柱内线速度为us，由于固定相对组分有保留作用，所以us ＜ u．此两速度之比称为滞留因子Rs。

通过选择因子α把实验测量值k与热力学性质的分配系数K直接联系起来，α对固定相的选择具有实际意义。如果两组分的K或k值相等，则α = 1，两个组分的色谱峰必将重合，说明分不开。两组分的K或k值相差越大，则分离得越好。因此两组分具有不同的分配系数是色谱分离的先决条件。

（二）塔板理论

塔板理论最早由Martin等人提出，将色谱柱比作一个精馏塔，沿用精馏塔中塔板的概念来描述组分在两相中的分配行为，同时引入理论塔板数作为衡量柱效率的指标。

该理论假定：

1．在柱内一小段长度H内，组分可以在两相间迅速达到平衡。这一小段柱长称为理论塔板高度H。

2．以气相色谱为例，载气进入色谱柱不是连续进行的，而是脉动式，每次进气为一个塔板体积（ΔVm）。

3．所有组分开始时存在于第0号塔板上，而且试样沿轴（纵）向扩散可忽略。

4．分配系数在所有塔板上是常数，与组分在某一塔板上的量无关。

如果有一长度为L的色谱柱，则色谱柱的理论塔板数为

（12－11）

从色谱流出曲线出发，可以证明理论塔板数与保留时间和半峰宽度有关

（12－12）

塔板理论是一个人为概念，虽然用这个理论计算的塔板数波动很大，但在衡量柱效时仍是十分有用的。n越大，H越小，色谱柱分离效果越好。由式（12－12）可见，tR越大,W1/2越小，理论塔板数越多，塔板高度越小，因而柱效能越高。

由于包括在tR的死时间tM不参与柱内的分配，所以往往是计算的塔板数很大，但色谱柱的实际分离效能并不好。特别是对流出色谱柱较早的（tR小）的组分更为突出。为此，提出以有效塔板数n有效和有效塔板高度H有效作为色谱柱的操作效能指标：

n有效 （12－13）

（12－14）

n有效和H有效能更真实的反映色谱柱分离的效果。

二．速率理论

塔板理论虽然给出了板高的概念，但没有找到影响板高的因素，也不能说明色谱峰为什么会展宽。速率理论就是在塔板理论的基础上，引入影响板高的动力学因素而导出的。速率理论方程为

（12－15）

式中u为载气线速度（cm/s），其余各项的物理意义说明如下：

1．A－涡流扩散项形成的塔板高度分量

（12－16）

为填充不规则因子，由柱中固定相颗粒不均匀性所决定；dp为固定相颗粒直径。

当组分随着流动相通过色谱柱时，由于固定相颗粒不均匀，同一组分的不同分子受到的阻力不同。因此组分分子在气相中形成紊乱的类似涡流的流动，使这些分子到达柱末端的时间不同，从而引起峰形变宽。为降低涡流扩散，需采用直径小，粒度均匀的固定相。

2．－纵向扩散形成的塔板高度分量

（12－17）

式中为弯曲因子。在填充柱中，由于固定相颗粒的存在，使分子自由扩散受到阻碍，扩散距离降低， ＝ 0.5 ~ 0.7。而在空心柱中，扩散无障碍， ＝ 1。Ds为组分分子在气相中的扩散系数。

纵向扩散是由于柱内存在浓度梯度引起的，其扩散方向与载气运动方向一致。Ds与组分和载气的分子量有关，分子量大的组分，Ds小；Ds与载气分子量的平方根成反比。采用分子量较大的载气（如N2）可使B项降低；增大u，使组分在柱中停留时间短，可降低色谱峰展宽。

3．Cu-传质阻力所形成的塔板高度分量

系数C包括气相传质阻力系数Cg和液相传质阻力系数Ci两项。

（12－18）

式中k为分配比，dl为固定相液膜厚度，Dl为组分在液相中的扩散系数。

气相传质阻力是组分由气相导气液二相界面进行浓度分配时形成的，从气相导气液界面所需时间越长，则传质阻力越大，引起峰形展宽越大。液相传质阻力是组分从气液界面渗入固定液内，达到平衡后再扩散到气液界面的传质过程，这一过程也会引起峰形展宽。

将式（16），（17），（18）代入式（15）得：

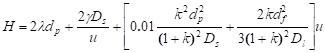（12－19）

式（12－20）称为范第姆特方程式或速率方程式，对分离条件的选择具有指导意义。

4．载气流速u对理论塔板高度的影响

由式（12－15）速率理论方程可得图12－3。曲线的最低点，板高最小，此时柱效最高。该点所对应的流速为最佳流速。将式（12－15）微分，并令其为零，得

（12－20）

实际工作中为加快分析速度，往往选择略大于的流速。A，B，C可通过如图12－3的实验曲线而求出。

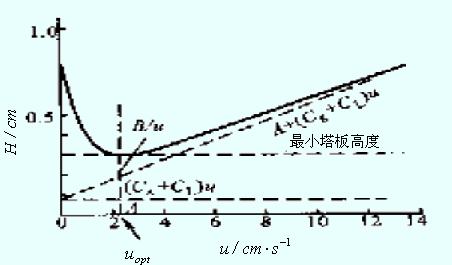
图12－3 塔板高度与载气流速的关系

二．色谱基本分离方程

被分析样品中各组分在色谱柱中能否得到分离，首先要选择适宜的固定相，其次要选择正确的分离条件。

（一）分离度

为判断相邻两组分在色谱柱中的分离情况，常用分离度（或称分辨率）R作为色谱柱的总分离效能指标。其定义为相邻两组分色谱峰保留值之差与其峰底宽度总和之半的比值：

（12－21）

由此可见，R值越大，相邻两组分分离得越好。从理论上可以证明，当R ＝ 1时，分离程度可达98％，R = 1.5时，分离程度可达99.7%。因而可用R = 1.5作为相邻二峰完全分开的标志（图12－4）。

由于两组分保留值的差别主要取决于固定液的热力学性质，色谱峰的宽窄则反映了色谱过程的动力学因素，柱效能的高低。因此分离度可作为色谱柱的总分离效能指标。

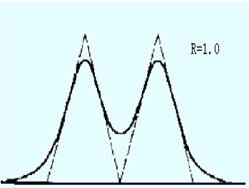
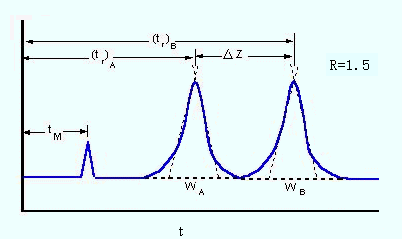
图12－4 不同分离度时色谱峰分离的程度

由于Wb难于测定，可用W1/2代替Wb，这时分离度的表示式为：

（12－22）

严格说，R并不等于R’，但二者相差极小，可近似地看作是相同的。

（二）色谱基本分离方程式

在色谱分析中，一般依据难分离物质对来确定塔板数，令Wb(1) = Wb(2) = Wb，则由式（21）得

或 （12－23）

将式（12－23）代入式（12－14），得

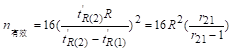（12－24）

例12-1 有一根 lm长的柱子，分离组分1和2。空气的保留时间为5s，组分1和2的保留时间分别为45和49s。如果Wb(1) = Wb(2) = 5s，试求该柱的分离度？如若使R = 1.2，，有效塔板数应为多少？色谱往要加到多长？

解：先求出组分2对组分1的相对保留值r2，1（即α值）

分离度

（块）

为使R＝1.2，所需塔板数

（块）

柱长应加到