一、问题解决的概念
    （一）什么是问题解决
    问题解决(problem solving)是由一定的情景引起的，按照一定的目标，应用各种认知活动、技能等，经过一系列的思维操作，使问题得以解决的过程。例如，证明几何题就是一个典型的问题解决的过程。几何题中的已知条件和求证结果构成了问题解决的情景，而要证明结果，必须应用已知的条件进行一系列的认知操作。操作成功，问题得以解决。
    20世纪70年代，纽厄尔和西蒙（Newell＆Simon，1972）通过对问题解决的计算机模拟，提出了“通用问题解决者模型”（general problem solver model），这一模型对问题解决的过程做出了详细的阐述。
    纽威尔和西蒙用问题空间(problem space)的概念说明问题解决的过程。问题空间是指问题解决者对所要解决的问题的一切可能的认识状态，包括对问题的初始状态和目标状态的认识，以及如何由初始状态转化为目标状态的认识等。他们认为，问题解决就是在问题空间进行搜索，以找到一条从问题的初始状态到达目标状态的通路。
    （二）问题的种类
    1．根据问题的明确程度，可分为界定清晰的问题(well-defined problem)和界定含糊的问题(ill-defined problem)。
    界定清晰的问题是指初始状态(initial state)、目标状态(goal state)以及由初始状态如何达到目标状态的一系列过程都很清楚的同题。例如，已知A>B，B<C．问A与C哪个大。界定含糊的问题是指对问题的初始状态或目标状态没有清楚的说明，或者对两者都没有明确的说明，这些问题具有很大的不确定性。例如“如何写一篇论文”，这个问题的初始状态和目标状态都是不清楚的。
    2．根据在问题解决时，问题解决者是否有对手，可分为对抗性问题(adversary problem)与非对抗性问题(non-adversary problem)
    在解决对抗性问题时，人们不仅要考虑自己的解题活动，而且这种活动还要受对手解题活动的影响。例如，象棋、围棋、桥牌、扑克等游戏都属于对抗性问题。非对抗性问题是指在解决问题时没有对手参与的问题。例如，解决代数问题、几何问题等都属于非对抗性问题。
    3．根据在问题解决时，解决者具有的相关知识的多少，问题又分为语义丰富的问题(semantic rich problem)和语义贫乏的问题(semantic impoverished problem)
如果解题者对所要解决的问题具有很多相关的知识，这种问题称为语义丰富的问题。例如，物理学家解决物理学方面的问题，这种问题对他们来说是语义丰富的问题。如果解题者对要解决的问题没有相关的经验，这种问题称为语义贫乏的问题。例如，初学物理的人解决物理学的问题，这种问题对于他们来说便是语义贫乏的问题。
    问题种类的划分是相对的，而不是绝对割裂的。例如，下象棋属于对抗性的问题；对于初学者来说，它是语义贫乏的问题；对于象棋专家来讲，它是语义丰富的问题。
    （三）问题解决中的策略
采用什么样的策略解决问题，是影响问题解决效率的一个很重要的心理因素。好的策略，有利于问题的解决。例如，9+3+2+7+8+1=?人们可以按顺序进行加法运算，但用这种方法解央问题的效率较低，且易出现错误。如果采用凑10的办法，就能迅速准确地解决问题了。
    纽厄尔和西蒙(1972)认为，在问题解决过程中，有如下几种通用的解决问题的策略：
    1．算法
    算法策略(algorithm strategy)就是在同题空间中随机搜索所有可能的解决问题的方法，直至选择一种有效的方法解决问题。简而言之，算法策略就是把解决同题的方法一一进行尝试，最终找到解决问题的答案。例如，一只密码箱有3个转钮，每一转钮有0～9十位数字，现要采用算法策略找出密码打开箱子，就要逐个尝试3个数字的随机组合，直到找到密码为止。采用算法策略的优点是它能够保证问题的解决，但是采用这种策略在解决某些问题时需要大量的尝试，因此费时费力。当问题复杂、问题空间很大时，人们很难依靠这种策略来解决问题。另外，有些问题也许没有现成的算法或尚未发现其算法，对这种问题算法策略将是无效的。
    2．启发法
    启发法(heuristic method)是人根据一定的经验，在问题空间内进行较少的搜索，以达到问题解决的一种方法。启发法不能完全保证问题解决的成功，但用这种方法解决问题较省时省力。下面是几种常用的启发性策略：
    其一，手段—目的分析
    所谓手段—目的分析(mean-end analysis)就是将需要达到的问题的目标状态分成若干子目标，通过实现一系列的子目标最终达到总目标。它的基本步骤是：①比较初始状态和目标状态，提出第一个子目标；②找出完成第一个子目标的方法或操作；③实现子目标；④提出新的子目标。如此循环往复，直至问题的解决。以河内塔问题为例(图8-4)

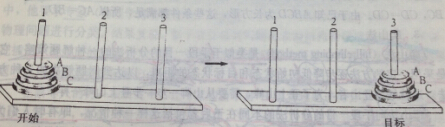
图8-4河内塔问题

    在一块板上有3根柱子，在柱1上有自上而下大小渐增的三个圆盘A、B、C。要求被试将圆盘移到柱3上，且仍保持原来放置的大小顺序。移动的条件是每次只能移动一个圆盘，大盘不能放在小盘上，在移动时可利用柱2。解决这一问题，目前最重要的差异是C盘不在柱3上，要消除这一差异，选择的操作是把C盘移到柱3上，但根据条，当C盘上没有其他圆盘时C盘才可移动，现在C上有B和A，因此建立的第二个子目标是先移动B。由于移动B的条件不成熟，因此另一个子目标是先移动A。现在，移动A的条件成熟，因此把A移到柱3，B移到柱2，再将A移到柱2B的上面，此时即可将C移到柱3上。这时当前状态与目标状态的差别是B不在柱3上，要消除这一差别，需建立另一个子目标，即先将A移到柱1，完成这一操作后，冉将B移到柱3上，最后把A移到柱3上。至此达到了问题所要求的目标状态。
    在日常生活中，手段—目的分析是人们比较常用的一种解题策略，它对解决复杂的问题有重要的应用价值。
    其二，逆向搜索
    逆向搜索(backward serch)就是从问题的目标状态开始搜索直至找到通往初始状态的通路或方法。例如，人们要去城市的某个地方，往往是在地图上先找到目的地，然后查找一条从目的地退回到出发点的路线。
    逆向搜索更适合于解决那些从初始状态到目标状态只有少数通路的问题，一些几何问题较适合采用这一策略。例如，“已知长方形ABCD，求证对角线AD= BC。运用逆向搜寻解决这一问题的思路是：要证明AD=BC，必须首先证明，△ACD≌△BCD；要证明两个三角形为全等三角形，必须证明∠ACD=∠BDC，AC = BD．CD=CD。由于已知ABCD为长方形，这些条件都满足，所以AD=BC。
    其三，爬山法
    爬山法(hlllclimbingmethod)是类似于手段一目的分析法的一种解题策略。它是采用一定的方法逐步降低初始状态和目标状态的距离，以达到问题解决的一种方法。这就好像登山者，为了登上山峰，需要从山脚一步一步登上山峰一样。
    爬山法与手段一目的分析法的不同在于后者包括这样一种情况，即有时人们为了达到目的，不得不暂时扩大目标状态与初始状态的差异，以有利于最终达到目标。
    （四）影响问题解决的心理因素
    问题解决除受策略、知识等因素影响外，还受到其他心理因素的影响。
    1．知识表征的方式
    知识的表征方式能影响问题的解决。例如，9点连线图问题。

图8-5九点连线图

    实验时要求将图中的9个点用不多于四条的直线一笔连在一起。人们常常不能成功地解决这一问韪，其原因在于，9个点在知觉上组成了方形，人们总是试图在这个方形的轮廓中连线，这样，知识的表征方式阻碍了问题的解决。如果在实验前告诉被试，连线时可以突破方形的限制，被试的成绩就会得到很大的提高。
    2．定势
    定势(set)是指重复先前的心理操作所引起的对活动的准备状态。它的影响有积极的，也有消极的。陆钦斯(Luchins，1942)在一个实验中，要求被试用人小不同的容器量出一定量的水，用数字进行计算（表7-2）。实验分两组，实验组从第1题做到第8题，控制组只做6，7，8三题。结果实验组在解1题—8题时，大多用B-A-2C的方法进行计算，称间接法。而控制组在解7，8题时，采用了简便的计算方式：A-C或A+C，称为直接法。这说明实验组在做7，8题时，受到了前面定势的影响，只有19%的人不受影响，而采用了直接法。
    3．功能固着
    人们把某种功能赋予某种物体的倾向称为功能固着（functional fixation），如盒子是装东西的，笔是写字的等等。在解决问题的过程中，人们能否改变事物固有的功能以适应新的问题情景的需要，常常成为解决问题的关键。在功能固着的影响下，人们不易摆脱事物用途的固有观念，因而直接影响到人们灵活地解决问题。杜克(Duncker，1945)的实验证实了这种影响。实验要求被试使用五种熟悉的工具解决五个新的问题。实验组在解决问题前对工具的习惯用法进行了练习，增加了功能固着的倾向。控制组直接解决问题。结果控制组的成绩大大超过了实验组（表7-4）。
    克服功能固着需要人们灵活机智地使用已有的工具或材料，使之服务于解决问题的目的，这称之为功能变通。功能变通与功能固着的作用相反。要具有这种能力，一方面需要有丰富的知识，要熟悉物体的不同功能，另一方面也要具有思维的灵活性。
    4．动机
    人们对活动的态度、社会责任感、认识兴趣等，都可以成为发现问题的动机，影响到问题解决的效果。动机的强度不同，影响的大小也不同。心理学家的实验表明，在一定的限度内，动机的强度和解决问题的效率成正比，但动机太强或太弱都会降低解决问题的效果。动机太强使人的心情过于紧张，不易发现解决问题的重要因素。动机太弱容易被无关因素引到问题之外。动机强度与解决问题效率之间的关系可以用一条倒U形曲线来说明。它表明在一定的范围内解决问题的效率，随动机强度的增高而上升，中等强度是解决问题的最佳水平。超过一定的限度，提高动机的水平，反而会降低解决问题的效率。
    5．情绪
    情绪对问题解决有一定的影响，紧张、惶恐、烦躁、压抑等消极的情绪会阻碍问题解决的速度，而乐观、平静、积极的情绪将有助于问题的解决。如学生考试时，由于情绪过分紧张，会使其思路阻塞，有时甚至面对容易的问题而束手无策。如果学生能以积极的情绪迎接考试，就特有利于思考，打开思路，使问题得以解决。
    6．人际关系
    人处在一个复杂的社会中，解决问题不仅受个人心理因素的影响，也要受到人们之间相互关系的影响。例如，人在解决问题时，往往要求与周围的人方式一致，这种现象称从众现象(conformity)。团体内的相互协作和互相帮助，是使问题得以迅速解决的积极因素；相反，互不信任、人际关系紧张则会妨碍问题的解决。
    （五）知识在问题解决中的作用——专家与新手的区别
    在日常生活中，各个领域都有自己的专家(expert)，如数学家、物理学家、医学专家、律师、象棋大师等。这些具有专门知识(domain-specific knowledge)的人，比新手(novice)或者专门知识较少的人，解决相应的问题要容易得多。是什么原因使得专家的问题解决更为容易呢？研究表明，专家和新手在知识的数量以及知识的组织方式上有所不同，可能是造成同题解决效率不同的主要原因。
    1．专家与新手在知识数量上的差异
    德格鲁特(De Groot，1965)在一系列著名的实验中，比较了国际象棋大师和普通棋手的差异。在一项研究中，给象棋大师和新手看实际比赛的棋局各5秒钟，然后打乱棋子的位置，让他们重新恢复棋局。结果发现，象棋专家正确恢复棋子的数量是20个—25个，而普通棋手只有6个。但当专家和新手所看的棋局为随机排列的棋局时，他们恢复棋子的数量没有差别，都是6个。彻斯等人（Chase et al．，1973）利用“组块”的概念解释了上述结果。他们认为，专家与新手相比，记忆存贮的信息量大，存贮熟悉的棋局模式多，这些差别决定了专家与新手棋艺水平的差别。
   有人(McKeithen et al．，1981)以计算机程序专家和新手为被试，要求他们记忆有意义的程序和无意义的程序（把有意义的程序随机混乱）。结果表明，在回忆有意义的程序时，专家的成绩好于新手，但在回忆无意义的程序时，专家的成绩并不比新手好。这同样说明，专家存贮的计算机程序的知识多于新手。
    2．专家与新手在知识组织方式上的差异
    专家与新手不仅在知识的数量上存在差别，而且在知识的组织方式上可能也存在差别。
    蔡等人（Chi et al．，l982）对专家和新手的知识组织方式进行了研究。在实验中，他要求专家（物理学博士研究生）和新手（学过一学期力学的大学生）对24个物理问题进行分类。结果发现，新手往往根据问题的表面结构特征进行分类。例如，把插图中有斜面的问题分为一类，而专家则根据问题的深层结构进行分类，即把解题时运用相同定理的问题归为一类。
    在蔡等人的另一项研究中，让专家和新手对40道物理题进行分类。实验过程分四步：第一步，被试只需对这些问题分组；第二步，将原来的分组再分为亚组；第三步，对划分出的亚组再进行详细的划分；第四步，被试重新检查最初划分的组，并应用合适的原则把它们合并起来。
    结果表明：两位专家都能运用某种一致性的原则对40个问题进行分组。例如，专家C和D，把20道题合并为守恒定律的问题，把另20道题合并为运动方程的问题。而在两位新手中，只有一位能够确定出上述类别，而且只能解释40个问题中的14个。这表明，专家的知识是按层次结构的方式组织起来的，这种组织方式是专家长期解题经验的结果。