当企业购买投入要素生产它们要销售的产品时，就会产生成本。在本节，我们将分析企业生产过程和它的总成本之间的联系。我们再次以卡洛琳的饼干厂为例。
　　在下面的分析中，我们做一个重要的假设，目的是简化分析：假设卡洛琳工厂的规模是固定不变的，卡洛琳改变饼干产量的唯一方法是改变她雇佣的工人数量。这个假设在短期是合理的，但在长期则不合理。也就是说，卡洛琳无法一晚上（短期）就建成一个更大的工厂，但若花一两年时间（长期）则可以建成。因此，这种分析，描述的是卡洛琳在短期中的生产决策。我们稍后再详细分析成本和时间维度的关系。
　　生产函数
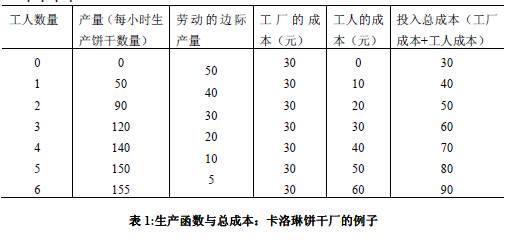
　　表 1 说明了卡洛琳饼干厂每小时饼干的产量与工人数量之间的关系。前两列的数据表明：若工人为0 个，产量为0；若工人为1 个，产量为50 单位的饼干；若工人为2 个，产量为90 单位的饼干，等等。图2 中的（a）图画出了这两列数字之间的关系图。工人数以横轴表示，饼干产量以纵轴表示。投入要素（工人劳动）数量和产出（饼干）量之间的关系称为生产函数（production function）。

　　第 1 章经济学十大原理中有一条是：人们在边际处思考。我们在后面章节将看到，这个原理是理解企业雇佣工人数量和产量决策的关键所在。为了向理解这些决策的目标靠近，b 表1 第三列给出了工人的边际产量。在生产过程中，任何投入要素的边际产量（marginal product）是指，额外增加一单位这种投入要素投入能够得到的产量增加量。当工人量由1变为2 时，饼干的产量从50 增加到90，因此第二个工人的边际产量是40 单位饼干。当工人数量由2 增加为3 时，饼干的产量从90 增加到120，因此第三个工人的边际产量是30 单位饼干。在表1 中，我们把边际产量放在两行之间，因为它代表当工人数量从一个水平增加到另外一个水平时产量的变化量。

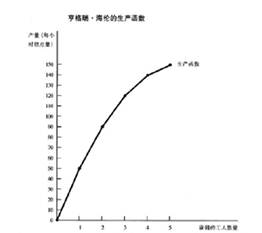
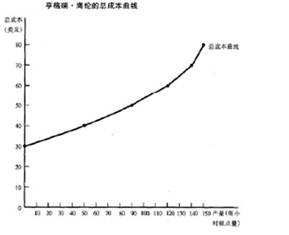
　　图2：卡洛琳的生产函数和总成本曲线。（a）图中的生产函数表明了工人数量和饼干产量之间的关系。在此图中，工人数量（横轴）来自表1 第一列，饼干的产量（纵轴）来自表1第二列。随着工人数量的增加，生产函数曲线变得越来越平坦，这表明边际产量递减。（b）图中的总成本曲线，表明了产量和总成本函数之间的关系。在此图中，产量（横轴）来自表1 的第二列，总成本（纵轴）来自表1 第六列。总成本曲线随着产量的增加而变得越来越陡峭，这是由于边际产量递减。
　　注意，随着工人数量增加，边际产量是下降的。第二个工人的边际产量为40 单位饼干，第三个工人的边际产量为30 单位，第四个工人的边际产量为20 单位。这种性质称为边际产量递减（diminishing marginal product）。最初，当只雇佣一两个工人时，他们更容易使用作坊生产设备。随着工人数量增加，额外增加的工人必须和先前的工人共用设备，而且在更为拥挤的空间中作业。最终，作坊变得很拥挤，工人彼此碍事。因此，随着工人数量增加，每个额外增加的工人对总产量的贡献越来越小。
　　边际产量递减在图2 中也很明显。生产函数的斜率（垂直量除以水平量）告诉我们，对于额外每单位劳动投入（水平量）带来的产量变化量（垂直量）。也就是说，生产函数的斜率衡量工人的边际产量。随着工人数量增加，边际产量递减，生产函数曲线越来越平缓。
　　从生产函数到总成本曲线
　　表 1 最后三列表明了卡洛琳生产饼干的成本。在这个例子中，卡洛琳工厂的成本为每小时30 元，工人的成本为每小时10 元。如果她雇佣1 个工人，她的总成本为每小时40 元。如果她雇佣2 个工人，她的总成本为每小时50 元，等等。根据这些信息，从表1 可以看出卡洛琳雇佣的工人数和饼干产量之间的关系以及工人数和总生产成本之间的关系。
　　我们在接下来几章的任务是研究企业的生产和定价决策。对于这个目的来说，表1 中的最重要关系是产量（第二列）和总成本（第六列）之间的关系。图2 中的（b）图画出了这两列数据的关系，其中产量位于横轴上，总成本位于纵轴上。这个图形叫做总成本曲线（total-cost curve）。
　　现在比较（b）图中的总成本曲线和（a）图中的生产函数曲线。这两条曲线是同一枚硬币的两面。随着产量增加，总成本曲线变得越来越陡峭，而生产函数变得越来越平缓。这两条曲线斜率变化的原因是相同的。较高的饼干产量意味着卡洛琳的作坊里的工人数量较多。
　　由于作坊比较拥挤，额外的每个工人贡献的产量较小，这反映了边际产量递减。因此，生产函数比较平坦。但换个角度考虑一下这个逻辑：当作坊比较拥挤时，生产额外一单位饼干需要更多的额外劳动，因此成本较大。所以，当产量较大时，总成本曲线比较陡峭。